Introduction to molecular orbit
A molecular orbital diagram, or MO diagram, is a qualitative descriptive tool explaining chemical bonding in molecules in terms of molecular orbital theory in general and the linear combination of atomic orbitals molecular orbital method in particular Qualitative MO theory was introduced in 1928 by Robert S. Mulliken and Friedrich Hund. A mathematical description was provided by contributions from Douglas Hartree in 1928 and Vladimir Fock in 1930.
Some points are given below to describe the molecular orbital theory and its applications in diatomic molecules.
Molecular Orbitals
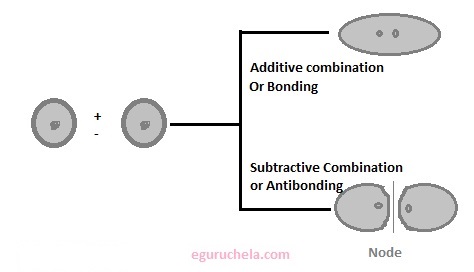
The region of an electron is likely to be found in a molecule. A MO is defined as the combination of atomic orbitals. This is to used for calculation of chemical and physical properties such as the probability of finding an electron in any specific region. It is the mathematical function describes the wave-like behavior of an electron in a molecule. The molecular orbitals are obtained by combining the atomic orbitals on the atoms in the molecule. For example consider the H2 molecule. One of the molecular orbitals in this molecule is constructed by adding the mathematical functions for the two 1s atomic orbitals that come together to form this molecule, it is also call additive combination or bonding. Another orbital is formed by subtracting one of these functions from the other called the subtractive combination or antibonding, as shown in the figure.
Homonuclear Diatomics
Molecules consisting of two identical atoms ,which are said to be homonuclear diatomic, such as: H2, N2, O2, and F2.
The diatomic molecules are linear and bond is non-polar due to the electronegativity difference of zero.
Heteronuclear Diatomics
Molecules consisting of two non-identical atoms are said to be heteronuclear diatomic, such as: CO, NO, HF, and LiF.
Bonding and Antibonding Orbitals
Orbitals that are out-of-phase with one of another are "antibonding" orbitals because regions with dense electron probabilities do not merge which destabilizes the molecule. "Bonding" orbitals are less energetic than antibonding atomic orbitals and are in-phase, as depicted in the figure below. Note how the bonding orbitals come together constructively, while the antibonding orbitals do not.
Phases and nodes
Phases are designated either (+) or (-) relative to their wave "up" or wave "down" displacements. A node occurs if the phase signs change from (+) to (-) or vice versa. It is important to notice that the phase signs do NOT symbolize charges. Nodes are regions where the probability of finding an electron is ZERO.
Sigma and Pi Bonds
A sigma-bond is an "end-to-end" bond formed from symmetric atomic orbitals. A pi-bond is formed from a "sideways" overlap.
MO theory in principle gives us a way to calculate the energies and wavefunctions of electrons in molecules very precisely, usually we settle for simplified models here too. These simple models do not give very accurate orbital and bond energies, but they do explain concepts such as resonance that are hard to represent otherwise. We can get more accurate energies from MO theory by computational "number crunching."
We use atomic orbitals (AO) as a basis for constructing MO's.
LCAO-MO = linear combination of atomic orbitals. In physics, this is called this the tight binding approximation.
Example of the LCAO-MO approach :
ψ1 = c1 φ1 + c2 φ2and
ψ2 = c1 φ1 - c2 φ2
Coefficients c1 and c2 will be equal (or nearly so) when the two AOs from which they are constructed are the same.
Go to index page
