Dispersion by a Prism
Visible light is actually made up of different colors.
Each color bends by a different amount when refracted by glass. That's why visible light is split, or dispersed, into different colors when it passes through a lens or prism.
Shorter wavelengths, like purple and blue light, bend the most.
Longer wavelengths, like red and orange light, bend the least.
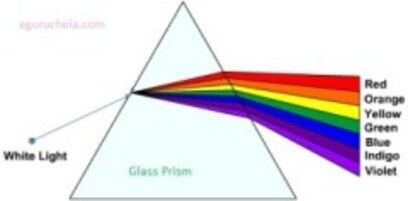
Dispersion of Light
The splitting of white light into its constituent colors in the sequence of Violet, Indigo ,Blue, Green, Yellow, Orange and Red (VIBGYOR) on passing through a prism is called dispersion of light.
The refractive index μviolet > μRed,
therefore violet color deviates most and red color deviates least. For example δviolet > δRed.
Angular Dispersion
The angle subtended between the direction of emergent violet and red rays of light from a prism is called angular dispersion. The angular dispersion produced by a prism for white light is the difference in the angles of deviation of two extreme colors (violet and red colors).
(θ) δV - δR = (µV - µR)Awhere δV the angle deviation of Violet and δR the angle deviation of Red
Refraction Through a Prism
The prism is denoted by A, B, C. Where BC is the base and AB and AC are its two refracting surfaces as shown in figure, we can say that OP is the incident. The ray traveling through the rarer medium and than the refractive index of the prism is the incident ray. As the ray PQ strikes the surface of the and it is called as the refracted ray. OR is the emergent ray which comes out.
The ray light bends towards normal when it enters the glass and when ray comes out, it bends away from the normal.
Now the angle between the emergent ray and incident ray is the angle of deviation.
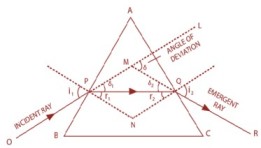
For a single refracting surface, δ = |i – r|
In this case, δ = (i1 + i2) – (r1 + r2)
δ = i1 + i2 – A, A is the angle between the prism between two lateral surfaces. We know that ∠A and ∠Q is 180º and Angle of the prism of (A) is r1 + r2
The r1 is angle of refraction inside the prism and r2 is the angle of refraction outside it. For an angle of minimum deviation; δ is minimum and i1 = i2 = i
δmin = 2i – A
For small A, δ = (µ – 1) A
Examples of dispersion
The most familiar example of dispersion is probably a rainbow, in which dispersion causes the spatial separation of a white light into components of different wavelengths (different colors).
However, dispersion also has an effect in many other circumstances:
for example, group velocity dispersion (GVD) causes pulses to spread in optical fibers, degrading signals over long distances; also, a cancellation between group-velocity dispersion and nonlinear effects leads to soliton waves.

