eguruchela

AC Voltage Applied to an Inductor

Inductors are basically coils or loops of wire that are either wound around a hollow tube former (air cored) or wound around some ferromagnetic material (iron cored) to increase their inductive value called inductance. Inductors store their energy in the form of a magnetic field that is created when a DC voltage is applied across the terminals of an inductor.

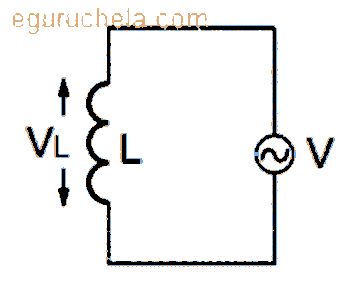
AC Voltage Applied to an Inductor

The voltage in an inductor can be measured as the EMF (amount of Electro Motive Force) generated for the change of current.

AC voltage applied to an inductor derivation

The flow of AC current through an indicator can be examine using Lenz’s law.

When the current rises from zero to maximum value then the magnetic field and current of the coil getting increase. Therefore an induced EMF is found with its direction as stated by the Lenz’s Law :

$$ E = -\frac{d \phi}{dt} $$

In some cases when the current declines from peak value to zero then magnetic field of the coil also becomes zero. Therefore the relation of the induced EMF is as:

$$ E = −L\frac{di}{dt} $$

It is known that ф = L × i

The voltage required by AC source is: $$ V = L × \frac{di}{dt} $$ The relation between current and voltage (across the coil) is :

$$ V = L × \frac{di}{dt} $$ $$ \frac{di}{dt} = \frac{V}{L} $$ $$ \frac{di}{dt} = \frac{V_{m}sin \omega t}{L} ---- 1 $$

Where, Vm = Maximum voltage and \omega = Angular frequency.

by integrating equation number 1
$$ i = ∫\frac{V_{m}sin \omega t}{L}dt $$ $$ i = \frac{−V_{m}cos \omega t}{\omega L} $$ $$ i = \frac{V_{m}sin( \omega t − \frac{\pi}{2})} {ωL} $$ $$ i = i_{m}sin(\omega t− \frac{\pi}{2}) $$

Where, im = Maximum value of current

therefore relation for inductive reactance

$$ V = V_{m}sin⁡ \omega t $$ $$ i = i_{m}sin( \omega t− \frac{\pi}{2}) $$ $$ i = -i_{m}cos ⁡\omega $$ $$ i_{m} = \frac{V_{m}}{\omega _{L} } $$ $$ i_{m} = \frac{V_{m}}{X_{L}} $$

From above expression, Inductive reactance = XL

Inductors do not behave the same as resistors. Whereas resistors simply oppose the flow of electrons through them (by dropping a voltage directly proportional to the current), inductors oppose changes in current through them, by dropping a voltage directly proportional to the rate of change of current.

In accordance with Lenz’s Law, this induced voltage is always of such a polarity as to try to maintain current at its present value.

reaccurr.jpg

That is, if current is increasing in magnitude, the induced voltage will “push against” the electron flow; if current is decreasing, the polarity will reverse and “push with” the electron flow to oppose the decrease.

This opposition to current change is called reactance, rather than resistance.

Types of inductors

Air-core Inductor.

Iron-Core Inductor.

Toroidal Inductors.

Laminated Core Inductors.

Powdered Iron Core Inductors.