AC Voltage Applied to a Resistor
When we apply an ac voltage to a resistor as shown to the right, current will flow through that resistor. This much seems logical and reasonable. But how much current? Can we apply Ohm's Law as we did with DC? How can we even specify the ac voltage, since it is constantly changing? To answer these questions, we must first define how we will specify the ac voltage applied to the resistor.
AC voltage source is nothing but Alternative Current voltage source, by its name it self we came to know that the current from AC voltage source is alternative one i.e., which will change over time. Where as in DC voltage source the current from DC voltage source is constant over time.
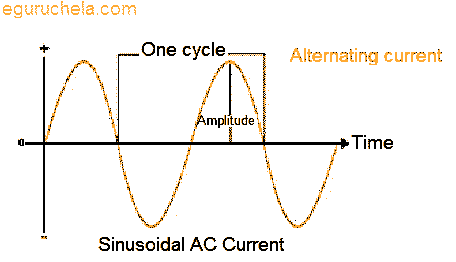
The current is called alternating current if source is producing current which varies with time periodically .As shown, considering that the source is producing sinusoidal varying potential difference (voltage) across its terminals. This can represent as:
V = Vmsin ωt
Where
Vm = Amplitude of the oscillating potential difference
ω = Angular frequency.
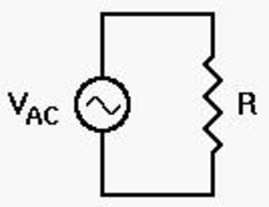
AC voltage applied to a resistor derivation
The current through the resistor due to the present voltage source can be calculated by apply the Kirchhoff's loop rule as:
∑V(t) = 0
Using this equation,can be writtten as:
V = Vmsin ωt = iR
Or
i = (Vm/R)sin ωt
Where
i = current and
R = resistance of the given resistor.
As per ohm's law,
V = iR or i = V/R
Ohm's law applicable where the source is producing AC or DC Voltage. therefore above equation can be written as:
im = Vm/R
By using this equation we can write i = (Vm/R)sin ωt
i = im sin ωt
In most cases, it makes a lot of sense to describe ac voltage and current in terms of a "dc equivalent," such that the actual ac power delivered to the load does exactly the same amount of work as the same value of dc voltage and current applied to the same load. To do this, we need to find some sort of "average ac power" over the entire cycle. Unfortunately, the actual average voltage of the applied ac is zero. The same is true of the alternating current flowing back and forth through the circuit. Yet we know that real power is used, because light bulbs turn on, clocks run, electric motors work, etc.
