Deviation from ideal behavior
The behavior of real gases usually agrees with the predictions of the ideal gas equation to within +- 5% at normal temperatures and pressures. At low temperatures or high pressures, real gases deviate significantly from ideal gas behavior. In 1873, while searching for a way to link the behavior of liquids and gases, the Dutch physicist Johannes van der Waals developed an explanation for these deviations and an equation that was able to fit the behavior of real gases over a much wider range of pressures.
Van der Waals realized that two of the assumptions of the kinetic molecular theory were questionable. The kinetic theory assumes that gas particles occupy a negligible fraction of the total volume of the gas. It also assumes that the force of attraction between gas molecules is zero.
The first assumption works at pressures close to 1 atm. But something happens to the validity of this assumption as the gas is compressed. Imagine for the moment that the atoms or molecules in a gas were all clustered in one corner of a cylinder, as shown in the figure below. At normal pressures, the volume occupied by these particles is a negligibly small fraction of the total volume of the gas. But at high pressures, this is no longer true. As a result, real gases are not as compressible at high pressures as an ideal gas. The volume of a real gas is therefore larger than expected from the ideal gas equation at high pressures.
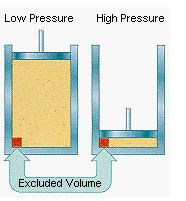
Van der Waals proposed that we correct for the fact that the volume of a real gas is too large at high pressures by subtracting a term from the volume of the real gas before we substitute it into the ideal gas equation. He therefore introduced a constant
constant (b) into the ideal gas equation that was equal to the volume actually occupied by a mole of gas particles. Because the volume of the gas particles depends on the number of moles of gas in the container, the term that is subtracted from the real volume of the gas is equal to the number of moles of gas times b.
P(V - nb) = nRT
When the pressure is relatively small, and the volume is reasonably large, the nb term is too small to make any difference in the calculation. But at high pressures, when the volume of the gas is small, the nb term corrects for the fact that the volume of a real gas is larger than expected from the ideal gas equation.
The assumption that there is no force of attraction between gas particles cannot be true. If it was, gases would never condense to form liquids. In reality, there is a small force of attraction between gas molecules that tends to hold the molecules together. This force of attraction has two consequences:
(1) gases condense to form liquids at low temperatures and
(2) the pressure of a real gas is sometimes smaller than expected for an ideal gas.
Possible deviations from the ideal behaviour
As we know that under high pressure, the deviation is very large and the magnitude of the volume of the gas decreases as compared to its container and the intermolecular attraction is strong.
Deviation varies from gas to gas. As we know that CO2 deviates at very low pressure and do not show any sign of ideal gas behaviour.
Deviation is more when the temperature decreased and gas becomes liquid with the maximum deviation.
The gas Xenon (Xe) has the largest element size. terefore it is assumed that Xenon gas will deviate the most when put under high pressure and low temperature.
