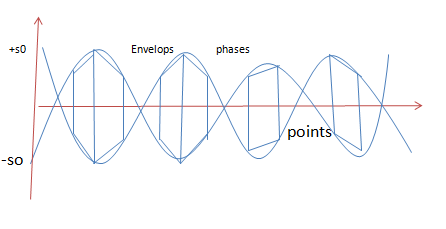
Phase and Group velocities
Phase and group velocity are two important and related concepts in wave mechanics. The ambiguity in the definition of "wave velocity" often leads to confusion, and we frequently read stories about experiments purporting to demonstrate "superluminal" propagation of electromagnetic waves (for example). Invariably, after looking into the details of these experiments, we find the claims of "superluminal communication" are simply due to a failure to recognize the differences between phase, group, and signal velocities.
The phase velocity is given in terms of the wavelength λ and period T as Vp = Λ/T
Equivalently, in terms of the wave's angular frequency ω, which specifies angular change per unit of time, and wavenumber (or angular wave number) k, which represents the proportionality between the angular frequency ω and the linear speed (speed of propagation) νp,
The angular frequency Ω of a wave is the number of radians per unit time at a fixed position, whereas the wave number k is the number of radians per unit distance at a fixed time.
A(t,x) = A0 cos(kx - Ωt)