Newton's law of cooling
Newton's law of cooling states that the rate of heat loss of a body is proportional to the difference in temperatures between the body and its surroundings. As such, it is equivalent to a statement that the heat transfer coefficient, which mediates between heat losses and temperature differences, is a constant. This condition is generally true inthermal conduction (where it is guaranteed by Fourier's law), but it is often only approximately true in conditions of convective heat transfer, where a number of physical processes make effective heat transfer coefficients somewhat dependent on temperature differences. Finally, in the case of heat transfer by thermal radiation, Newton's law of cooling is not true.
the temperature of a hot object (T1) which is cooling down as a result of exposure to a convective flow at T2 < T1, would vary as:
$$ \frac{DT _{1}}{dt} = (T _{1} - T _{2}) $$If the energy loss from the hot body to the cooler fluid is replenished by a heat flux q such that T1 remains constant then the steady state version of Newton's Law of Cooling can be expressed as
$$ q \propto (T _{1} - T _{2}) = \propto{(T _{1} - T _{2})} $$
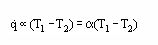
This rate equation is universally used to define the Heat Transfer Coefficient (α) for all convective flows (free, forced, single/multiphase, etc.) involving either heating or cooling. It should be noted that in some cases (α) is temperature dependent and then is not a linear function of the driving force (T1 – T2).
It should also be noted that the defining driving force varies from system to system (boundary layer flows, tube flows, etc.), but the complexity of any particular process is usually reflected in the formulation of the expression for (α), whose value depends upon the nature and properties of the flow system and ranges from 10 W/m2K for Natural Convection between air and a vertical plate to 100,000 W/m2K for dropwise Condensation of saturated water vapor at a vertical plate.
