Packing efficiency
The CCP and HCP are highly efficient lattice in terms of packing. The packing efficiency of both types of close packed structure is 74%, i.e. 74% of the space in hcp and ccp is filled. The hcp and ccp structure are equally efficient; in terms of packing.
The packing efficiency of simple cubic lattice is 52.4%. And the packing efficiency of body centered cubic lattice (bcc) is 68%.
packing efficiency or packing fraction is the fraction of volume in a crystal structure that is occupied by constituent particles. It is dimensionless and always less than unity. In atomic systems, by convention, the APF is determined by assuming that atoms are rigid spheres. The radius of the spheres is taken to be the maximal value such that the atoms do not overlap.
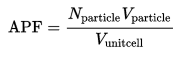
where Nparticle is the number of particles in the unit cell, Vparticle is the volume of each particle, and Vunit cell is the volume occupied by the unit cell. It can be proven mathematically that for one-component structures .
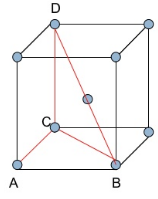
The Packing efficiency of body centered cubic (bcc) structure:
One atom is present in body center apart from 4 atoms at its corners. The total number of atoms present in bcc(body centered cubic) unit cell is equal to 2.
In the closest-packed structure, volume of the hexagonal unit cell is the product of the area and the height of the cell. The atoms at the corners of base of the unit cell are in contact, thus a = b = 2 r.
The height of an HCP unit cell
The height of the unit cell is taken as 4r in the packing efficiency of hcp arrangement.
The packing efficiency of diffrent type of unit cells and nearest neighbouring atoms as follows:
| Type of unit cell, lattice | Packing Efficienct | Void Space | No. of atoms in unit cell | Coordination Number | Relation between a and r | 1st nearest atom | 2nd nearest atom | 3rd nearest atom |
| Simple Cubic (SSC) | 52.4% | 47.6% | 1 | 6 | a = 2r | a along the edge of lattice | a√2 along the face of diagonal | a√3 along the body diagonal |
| Body Centred Cubic (BCC) | 68% | 32% | 2 | 8 | a = (4/√3)r | (√3/2)a along the body diagonal | a along the edge of lattice | a√2 along the face of diagonal |
| Face Centred Cubic (FCC) | 74% | 26% | 4 | 12 | a = 2√2r | a/√2 along the face diagonal | a along the edge of lattice | a√2 along the face diagonal |
