Crystal System Structure
Crystal systems, crystal families, and lattice systems are similar but slightly different, and there is widespread confusion between them: in particular the trigonal crystal system is often confused with the rhombohedral lattice system, and the term "crystal system" is sometimes used to mean "lattice system" or "crystal family".
A crystal system is a set of point groups in which the point groups themselves and their corresponding space groups are assigned to a lattice system. Of the 32 point groups that exist in three dimensions, most are assigned to only one lattice system, in which case the crystal system and lattice system both have the same name. Crystals possess a regular, repetitive internal structure.
The concept of symmetry describes the repetition of structural features.
Crystals therefore possess symmetry, and much of the discipline of crystallography is concerned with describing and cataloging different types of symmetry.
Two general types of symmetry exist. These consist of translational symmetry and point symmetry.
Translational symmetry describes the periodic repetition of a structural feature across a length or through an area or volume.
Point symmetry, on the other hand, describes the periodic repetition of a structural feature around a point. Reflection, rotation, and inversion are all point symmetries.
Lattices
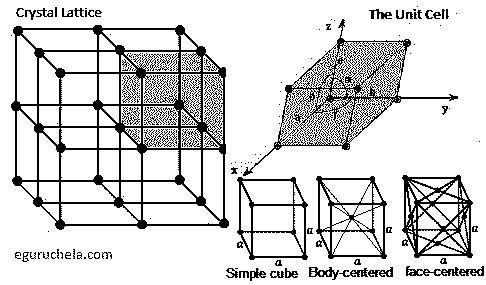
The unit cell of a lattice is the smallest unit which can be repeated in three dimensions in order to construct the lattice.
In a crystal, the unit cell consists of a specific group of atoms which are bonded to one another in a set geometrical arrangement.
This unit and its constituent atoms are then repeated over and over in order to construct the crystal lattice.
The surroundings in any given direction of one corner of a unit cell must be identical to the surroundings in the same direction of all the other corners.
The corners of the unit cell therefore serve as points which are repeated to form a lattice array; these points are termed lattice points.
Bravais Lattices
The Bravais lattices are furthermore of three different types.
A Simple cubic or primitive lattice has only a lattice point at each corner of the three-dimensional unit cell.
A body-centered lattice contains not only lattice points at each corner of the unit cell but also contains a lattice point at the center of the three-dimensional unit cell.
A face-centered lattice possesses not only lattice points at the corners of the unit cell but also at either the centers of just one pair of faces or else at the centers of all three pairs of faces.
Crystals are formed by stacking the molecules. The fourteen Bravais lattices may be divided among six crystal systems.
These crystal structure = lattice + basis as follows:
| Crystal Systems | Structure | Examples | Angles | Lengths |
|---|---|---|---|---|
| Isometric or Cubic | 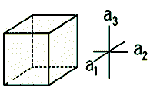 |
Au, Cu, NaCl | α = β = γ = 90∘ | a = b = c |
| Tetragonal | 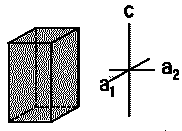 |
TiO2, SnO2, NiSO4 | α = β = γ = 90∘ | a =b ≠ c |
| Orthorhombic | 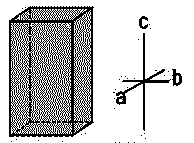 |
KNO3, BaSO4 | α = β = γ = 90∘ | a ≠ b ≠ c |
| Monoclinic | 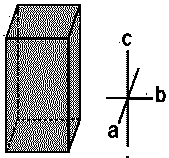 |
FeSO4, Na2SO4 | α = β = 90∘ ≠ γ | a ≠ b ≠ c |
| Triclinic | 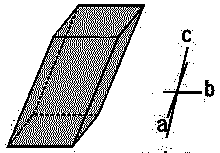 |
K2Cr2O7 | α ≠ β ≠ γ | a ≠ b ≠ c |
| Hexagonal | 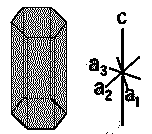 |
SiO2, Zn, Mg, Cd | α = β = 90∘ α = β = 90∘ , γ=120∘ | a=b≠c |
Characteristic of crystals
Following properties are important since they determine the usages of crystals in the industry because crystals differ in physical properties:
Hardness,
Cleavage,
Optical properties,
Heat conductivity and
Electrical conductivity.
