Magnetism and Gauss’s Law
Gauss's law for magnetism is one of the four Maxwell's equations that underlie classical electrodynamics. It states that the magnetic field B has divergence equal to zero,[1] in other words, that it is a solenoidal vector field. It is equivalent to the statement that magnetic monopoles do not exist. Rather than "magnetic charges", the basic entity for magnetism is the magnetic dipole. magnetic field lines are continuous loops, all closed surfaces have as many magnetic field lines going in as coming out. Hence, the net magnetic flux through a closed surface is zero.
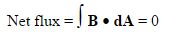
Gauss' Law for charges was a very useful method for calculating electric fields in highly symmetric situations. Gauss' Law for magnetism is considerably less useful, but we'll come up with another law that enables us to calculate magnetic fields in highly symmetric situations.
