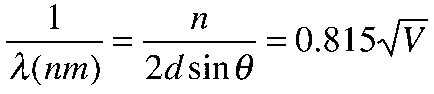Davisson and Germer Experiment
The Davisson-Germer experiment demonstrated the wave nature of the electron, confirming the earlier hypothesis of deBroglie.
Putting wave-particle duality on a firm experimental footing, it represented a major step forward in the development of quantum mechanics.
The Bragg lawfor diffraction had been applied to x-ray diffraction, but this was the first application to particle waves.
Davisson and Germer designed and built a vacuum apparatus for the purpose of measuring the energies of electrons scattered from a metal surface. Electrons from a heated filament were accelerated by a voltage and allowed to strike the surface of nickel metal.
Three years after de Broglie asserted that particles of matter could possess wavelike properties, the diffraction of electrons from the surface of a solid crystal was experimentally observed by C. J. Davisson and L. H. Germer of the Bell Telephone Laboratory.
In 1927 they reported their investigation of the angular distribution of electrons scattered from nickel.
With careful analysis, they showed that the electron beam was scattered by the surface atoms on the nickel at the exact angles predicted for the diffraction of x-rays according to Bragg's formula, with a wavelength given by the de Broglie equation:
λ = h / mv.
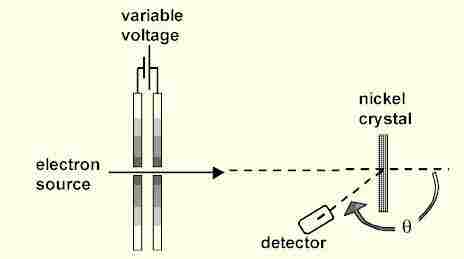
The experimental data above, reproduced above Davisson's article, shows repeated peaks of scattered electron intensity with increasing accelerating voltage.
This data was collected at a fixed scattering angle.
Using the Bragg law, the deBroglie wavelengthexpression, and the kinetic energy of the accelerated electrons gives the relationship. In the historical data, an accelerating voltage of 54 volts gave a definite peak at a scattering angle of 50°.
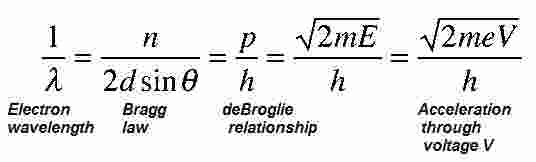
The angle theta in the Bragg law corresponding to that scattering angle is 65°, and for that angle the calculated lattice spacing is 0.092 nm. For that lattice spacing and scattering angle, the relationship for wavelength as a function of voltage is empirically