Damped simple harmonic motion
A physical system in which some value oscillates above and below a mean value at one or more characteristic frequencies. Such systems often arise when a contrary force results from displacement from a force-neutral positionand gets stronger in proportion to the amount of displacement, as in the force exerted by a spring that is stretched orcompressed or by a vibrating string on a musical instrument .
Observing the nature, we realize that many physical processes (for example, the Earth rotation around its polar axis) are repetitive, happening the facts cyclically. In these cases we speak about periodic motion and we characterize it by means of its period, which is the necessary time to complete a cycle, or by its frequency, which represents the number of complete cycles in the unit of time.
Damped Simple Harmonic Motion
When the motion of an oscillator decreases due to an external force, the oscillator and its motion get dampened. This harmonic motion of gradually decreasing amplitude is simple harmonic motion. The simple pendulum is an example of a damp simple-harmonic-motion, the energy of the oscillator dissipates continuously. The forces which dissipate the energy is generally frictional forces. The decrease in amplitude (or energy) of an oscillator is called damping and oscillation is called damping.
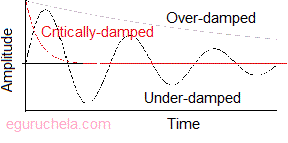
Overdamped
The system returns to equilibrium without oscillating.
Critically damped
The system returns to equilibrium as quickly as possible without oscillating.
Underdamped
The system oscillates (at reduced frequency compared to the undamped case) with the amplitude gradually decreasing to zero.
Undamped
The system oscillates at its natural resonant frequency (ωo) without experiencing decay of its amplitude.
Difference between simple harmonic motion and damped harmonic motion
In the case of simple harmonic motion, in a simple undriven harmonic oscillator, the only force acting on the mass is the restoring force. The simple harmonic motion(SHM) is the oscillatory motion for a system that can only be described by Hooke's law. Such a system is also called simple harmonic oscillator.
In the case of damped harmonic motion, in a damped harmonic oscillator there is additionally a frictional force that is always in the direction opposing the motion. Some examples are, weight on a spring, swinging pendulum and RLC circuit
