Ampere's Circuital Law
Ampère's law relates magnetic fields to electric currents that produce them. Ampère's law determines the magnetic field associated with a given current, or the current associated with a given magnetic field, provided that the electric field does not change over time.
In its original form, Ampère''s circuital law relates a magnetic field to its electric current source.
The law can be written in two forms, the "integral form" and the "differential form". The forms are equivalent, and related by the Kelvin–Stokes theorem.
It can also be written in terms of either the B or H magnetic fields. Again, the two forms are equivalent.
Ampère's circuital law is now known to be a correct law of physics in a magnetostatic situation:
The system is static except possibly for continuous steady currents within closed loops.
In all other cases the law is incorrect unless Maxwell's correction is included .
Ampere's Law states that for any closed loop path, the sum of the length elements times the magnetic field in the direction of the length element is equal to the permeability times the electric current enclosed in the loop.
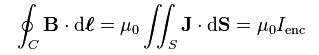
where J is the total current density (in ampere per square metre, Am-2)
And • is the vector dot product
dℓ is an infinitesimal element (a differential) of the curve C .
dS is the vector area of an infinitesimal element of surface S
Importance of Ampere's law
Ampere's Law allows to bridge the gap between electricity and magnetism and provides a mathematical relation between magnetic fields and electric currents.
Ampere's Law provide the way to calculate the magnetic field that is produced as a result of an electric current moving through a wire of any shape.
Applications of Ampere's law
Ampere's law can be used to know what magnetic field is generated by an electric current. This is useful in building electromagnets, motors, generators, transformers etc..
Limitation of Ampere's law
The limitation of Ampere's circuital law is that its only applicable in Magnetostatics or its only valid for the steady current.
Proof of Ampere's Circuital Law
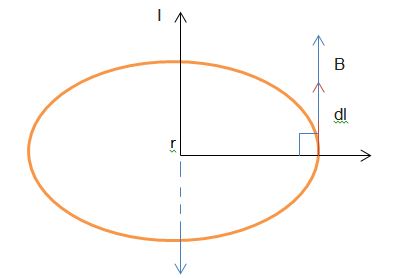
In the case of Regular Coil
Let's consider a regular coil carrying current I, assuming a small element dl on the loop.
∫B dl = ∫B dl cos θ
Where,
θ = small angle with the magnetic field. Since the magnetic field will be around the conductor therefore assume θ = 0°
As we know, due to a long current-carrying wire, magnitude of a magnetic field at point P at a perpendicular distance (r) from the conductor is :
B = μ0i / 2πr
As observed, magnetic field does not vary at a distance (r) due to symmetry. The integral of an element will form the whole circle (2πr):
∫ dl = 2πr
Apply the value of B and ∫ dl in the equation :
B∫ dl = (μ0i / 2πr) × 2πr = μoi
Hence, ∫ B.dl = μoi
In the case Irregular Coil
Means the coil of any arbitrary shape therefore radius (r) will not remain constant.
∫ B.dl1 = ∫ (μ0i / 2πr) × dl1
As we know :
dθ1 = dl1/r1
∴ ∫(μ0i/2πr) × dl1 = (μ0i / 2π) ∫dθ1 = μoi
∫ B.dl = μoi
The ampere's circuital law holds true both regular coil and irregular coil.
