Pythagorean Identities

---

The Pythagorean identities in trigonometry are the three identities that come from the Pythagorean theorem.

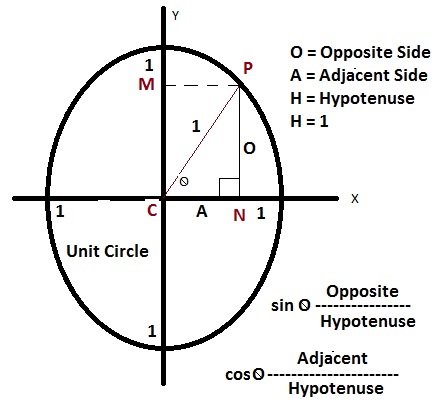
Proof of Pythagorean Identities :

Lets drow an unit circle as showing in picture and draw an angle θ since it is a unit circle so line CP = 1,

let draw the perpendicual lines to x and y axis as PN and PM.

As we know sinθ = opposite-side(O) / hypotunse and

cosθ = adjacent-side (A) / hypotunuse

since hypotunuse = radius = 1 herefore we can write as follows:

sinθ = O and cosθ = A

We know the Pythagorean theorem as:

CP² = PN² + CN² or 1² = O² + A²

Now replace the value of O and A with sinθ and cosθ; so we will get

1² = (sinθ)² + (cosθ)²
1 = sin²θ + cos²θ
sin²θ + cos²θ = 1 --------(1)
To prove other two indentities we can use following formulas:
           1 / sinθ = cscθ
           1 / cosθ = secθ
           sinθ / cosθ = tanθ
           cosθ / sinθ = cotθ
let take the basic indentity 1 = sin²θ + cos²θ and device both side by cos²θ
1 / cos²θ = sin²θ / cos²θ + cos²θ / cos²θ
1 / cos²θ = sin²θ / cos²θ + 1
apply basic formulas for 1 / cosθ = secθ and sinθ / cosθ = tanθ, then we will get
sec²θ = tan²θ + 1
1 + tan²θ = sec²θ -------------(2)
again take the basic indentity 1 = sin²θ + cos²θ and device both side by sin²θ
1 / sin²θ = sin²θ / sin²θ + cos²θ / sin²θ
1 / sin²θ = 1 + cos²θ / sin²θ
apply basic formulas for 1 / sinθ = cscθ and cosθ / sinθ = cotθ, then we will get
csc²θ = 1 + cot²θ
1 + cot²θ = csc²θ -------------(3)

Pythagorean Trig Identities

All the Pythagorean trig identities can be written in different forms by algebraic operations as follows:

• sin²θ + cos²θ = 1 ⇒ 1 - sin²θ = cos² θ ⇒ 1 - cos²θ = sin²θ
• sec²θ - tan²θ = 1 ⇒ sec²θ = 1 + tan²θ ⇒ sec²θ - 1 = tan²θ
• csc²θ - cot²θ = 1 ⇒ csc²θ = 1 + cot²θ ⇒ csc²θ - 1 = cot²θ

Formula for SOH CAH TOA

SOH : Sine = Opposite / Hypotenuse

CAH : Cosine = Adjacent / Hypotenuse

TOA : Tangent = Opposite / Adjacent