Perpendicular Bisector Equation Calculator
Calculate the perpendicular bisector for the line by putting the respective values on the x and y co-ordinates.
A perpendicular bisector is actually a line which intersects the given line at 90 degree or say it is the division of something into two equal or congruent parts. It may be a line, ray or segment which cuts another line segment into two equal parts at 90 degree.
The perpendicular bisector is a line that is cutting the line segment connected by two given points exactly in half by a 90 degree angle. The perpendicular bisector can be derived by following method:
First we derive the midpoint of the line using the midpoint formula as
[(x1 + x2 )/2,( y1 + y2 )/2].
The next we derive the slop of the line using the slope formula as
(y 2 - y1 ) / (x 2 - x1 ).
The next we determine the slope of the perpendicular bisector knowing that the slopes of perpendicular lines are opposites and reciprocals of each other.
The next we derive the perpendicular bisector equation (the equation with the slope and the midpoints) using formula y – y1 = m(x – x1) where y1 and x1 are the coordinates of midpoint.
And finally Solve the point-slope equation for y to get y = mx + b where x and y coordinates in the line are represented by the "x" and "y," the "m" represents the slope of the line and the "b" represents the y-intercept of the line.
/p>
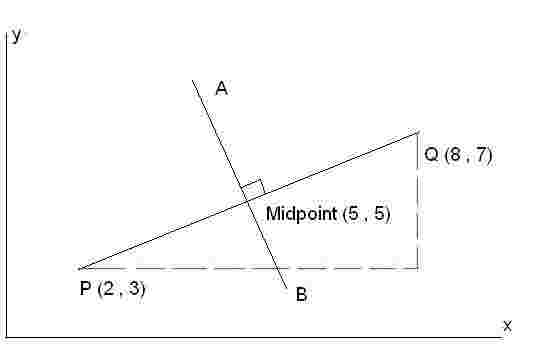
Lets understand the same thing with example. Find out the perpendicular bisector for given coordinates (2 , 3) and (8, 7).
1. Let find out the midpoint for given coordinates as follows:
[(2+8)/2, (3 +7)/2]
= (10/2, 10/2)
= (5, 5)
The midpoint coordinates are (5, 5) means (x1 , y2)
2. Find the slop of line for given coordinates as follows:
(7-3)/(8-2)
= 4/6
= 2/3
3. Find the negative reciprocal as follows
2/3
= 3/2
= -3/2 (m)
4. Now find the perpendicular bisector equation as follows:
y – y1 = m ( x – x1)
y – 5 = -3/2 (x – 5)
y – 5 = -3/2x + 15/2
y = - 1.5x + 7.5 + 5
y = -1.5x + 12.5