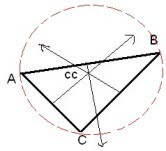
Circumcenter of Triangle, Bisector Calculation
The calculator calculates the circumcenter of a triangle for the entered values of the x and y co-ordinates.
The point where the perpendicular bisectors of triangle meets, is known as circumcenter.
We can say that circumcenter is the point of concurrency of the three perpendicular bisectors of each side of the triangle.
It is the point in the plane equidistant from the three vertices of the triangle.
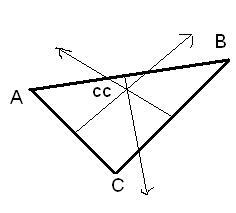
Calculate the midpoint of the sides AB, BC and CA which is the average of the x and y co-ordinates. Midpoint of a line in the triangle using formula :
$$ \frac{x1+x2}{2}, \frac{y1+y2}{2} $$
Midpoint of AB
Midpoint of BC
Midpoint of CA
Calculate the slope (m) of the sides AB, BC and CA using the formula:
$$ \frac{y2-y1}{x2-x1} $$
Slope of AB (m)
Slope of BC (m)
Slope of CA (m)
Calculate the slope of the perpendicular bisector of the lines AB, BC and CA.using formula:
$$ \text{The slope of the perpendicular bisector} $$
$$ = \frac{-1}{\text{slope of the line}} $$
Slope of the perpendicular bisector of AB
Slope of the perpendicular bisector of BC
Slope of the perpendicular bisector of CA
Find the equation of the perpendicular bisectors of the lines.
$$ \text{Formula to find the circumcenter equation:} $$
$$ y-y1 = m(x-x1) $$
Find the value of x and y by solving any two equations found in step 4 that will be the coordinates of the Circumcenter (cc) as shown in fig: