Orthocenter of Triangle, Altitude Calculation
Calculate the orthocenter of a triangle with the entered values of coordinates.
The orthocenter of a triangle is described as a point where the altitudes of triangle meet and altitude of a triangle is a line which passes through a vertex of the triangle and is perpendicular to the opposite side, therefore three altitudes possible, one from each vertex. We can say that all three altitudes always intersect at the same point is called orthocenter of the triangle.
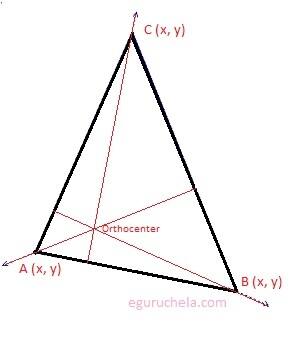
In the case triangle is obtuse (the triangle where one of the internal angles is greater than 90 degrees) than orthocenter will be outside. therefore we can say that orthocenter is not always inside the triangle.
There is 4 steps to calculate the orthocenter of any triangle as described below.
Step 1: Calculate the slope of the sides of the triangle using following formula: $$ \text{Slope of a line} = \frac{y\,_{2}-y\,_{1}}{x\,_{2}-x\,_{1}}$$ Step 2: Calculate the perpendicular slope of the sides using following formula: $$ \text{Perpendicular slope of the line } = \frac{-1}{ \text{Slope of a line} }$$ Step 3: Calculate the equation for any two altitudes with their respective coordinates using following formula: $$ y - y\,_{1} = m(x-x\,_{1})$$ Step 4: Solving altitude equations (any two altitude equation of Step 3)
