eguruchela

Midpoint (3 dimension) Calculator

Calculate the midpoint between two Entered coordinates (x1 , y1 , z1) and (x2 , y2 , z2) in three dimensional Cartesian coordinate system by averaging the XYZ coordinates.

Entered coordinates
A :
B :


The Midpoint Between (x1 , y1, z1 ) and (x2 , y2, z2) points measure a linear midpoint between two locations.

Midpoint Formula:

M = ((x1 + x2)/2 , (y1 + y2)/2 , (z1 + z2)/2)

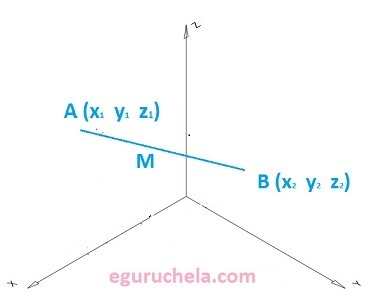
midp3.jpg

Therefore we can define the Midpoint with three dimention as follows:

The line segment on the 3D coordinate plane AB is a part of the line that is bound by two distinct points A(x1,y1,z1) and B(x2,y2,z2) which are called the endpoints of the line segment AB.

The point M is the midpoint of the line segment AB if it is an element of the segment and divides it into two congruent segments, AM and MB.

Each segment between the midpoint M and an endpoint have the equal length.

The midpoint is the center, or middle, of a line segment. Any line segment has a unique midpoint.

So, we can find the midpoint of any segment on the coordinate plane by using the mipoint formula.

$$ M(x_M,y_M,z_M)\equiv M(\frac{x_A + x_B }{2}, \frac{y_A + y_B}{2}, \frac{z_A + z_B }{2})$$ $$ or\equiv (\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}, \frac{z_1 + z_2}{2})$$