Centroid of a triangle Calculator
Calculator finds the coordinates on the centroid of a triangle for entered coordinates of the 3-vertices.
Properties of Centroid
Centroid is defined as the centre of the object.
Centroid always lie inside the object.
Centroid is also the centre of gravity.
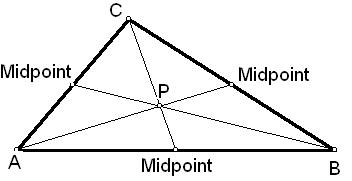
Centroid is the point of concurrency of all the medians.
The point through which all the three medians of a triangle pass is called Centroid of triangle. The each median connecting a vertex with the midpoint of the opposite side. It is also called the center-of-gravity of the triangle or as the barycent.
The coordinates of the centroid are the average of the vertices-coordinates.
Centroid of a Triangle Formula:
(( x1 + x2 + x3 )/3 , (y1 + y2 + y3 )/3).
Where
(x1, y1) – Coordinates of A
(x2, y2) – Coordinates of B
(x3, y3) – Coordinates of C